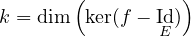
pour k < n, montrer qu’il existe des réflexions r1, ,rp (avec p ≤ n − k)
telles que
,rp (avec p ≤ n − k)
telles que
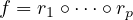
Énoncé
(Eao09) Soit E un espace euclidien de dimension n.
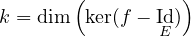
pour k < n, montrer qu’il existe des réflexions r1, ,rp (avec p ≤ n − k)
telles que
,rp (avec p ≤ n − k)
telles que
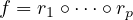
Corrigé
(Cao09)
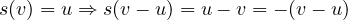
donc s est la réflexion par rapport à l’hyperplan Vect(v − u)⊥.
Synthèse. Soit s la réflexion par rapport à l’hyperplan Vect(v −u)⊥.
Alors :
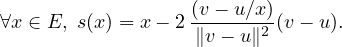
En particulier :
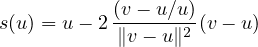
avec ∥v∥ = ∥u∥ donc
 |
On en déduit s(u) = v.