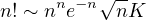Énoncé
(Eap02)
Formule de Stirling.
Pour n dans N∗, on pose Sn = ln(n!) et
- Montrer que 0 ≤ xn.
- Calculer un développement de xn+1 − xn dont le reste est o(
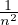 ).
).
- Calculer un développement de yn+1 − yn dont le reste est o(
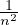 ).
).
- Montrer que la suite est monotone à partir d’un certain rang, montrer
ensuite qu’elle est convergente. En déduire l’existence d’un réel K tel
que
(voir exercice ip03 (http://81.28.96.244/data/temptex/fexip.pdf) pour une expression de
K.)
Corrigé
pas encore de corrigé
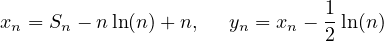
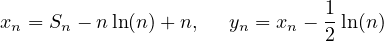
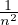 ).
).
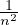 ).
).