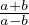 ,
, 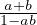 .
.
Énoncé
(Ecp01)
Soit a = eiα, b = eiβ simplifier 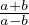 ,
, 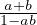 .
.
Corrigé
(Ccp01) Les formules suivantes sont souvent utiles :
| α | = 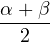 + + 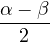 | ||
| β | = 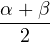 − −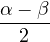 |
car elles permettent de factoriser une somme ou une différence d’exponentielles.
On peut mettre en facteur l’exponentielle de la somme et obtenir un sin ou un
cos.
| a + b | = ei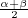 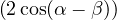 | ||
| a − b | = ei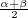 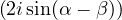 |
De même avec 0 comme argument de l’exponentielle :
| 0 | = 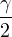 − −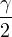 | ||
| γ | = 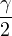 + + 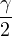 |
ce qui donne
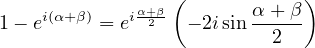
On en déduit :
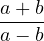 | = −i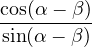 | ||
 | = i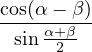 |