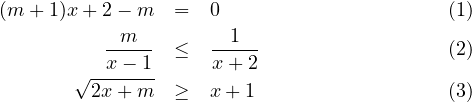
Énoncé
(Ecu01) Discuter et résoudre, suivant les valeurs du paramètre m, les équations ou inéquations
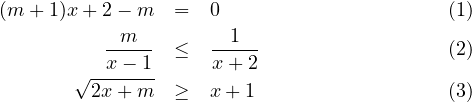
Corrigé
(Ccu01) Comme il s’agit de discuter sur le paramètre m, le résultat doit être de la forme suivante
Il ne doit JAMAIS apparaitre quelque chose du genre « Si x ceci alors ... »
On doit transformer l’équation ou l’inéquaion proposée en une autre équivalente
et d’une forme plus commode pour la résolution.
Étude de l’équation (1).
On peut discuter et répondre directement
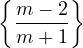
Étude de l’inéquation (2).
On transforme l’inéquation
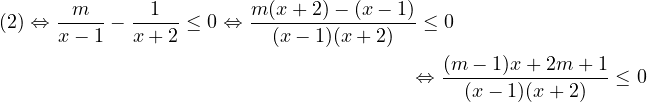 |
Lorsque m − 1≠0, on peut factoriser encore et tout revient à placer
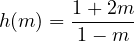
par rapport à −2 et 1. On étudie la fonction h ainsi définie. Il s’agit
d’une fonction homographique dont les propriétés suivantes doivent être
connues.
On peut la décomposer
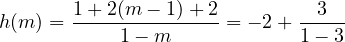
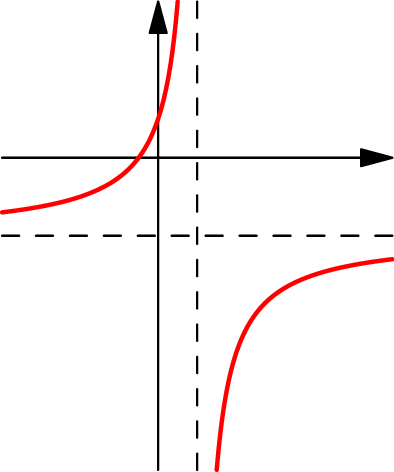
Son graphe (figure 1) est une hyperbole et elle est strictement croissante dans chaque intervalle de définition. De plus h(m) = 0 est impossible et h(m) = 1 ⇔ m = 0. Tout revient à étudier le signe de
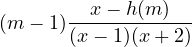
![]− 2,h(m)]∪ [0,+ ∞ [](Aexo_cu016x.png)
Ceci contient le cas particulier ] − 2,+∞[ pour m = 0.
![]− 2,1[∪ [h(m ),+ ∞ [](Aexo_cu017x.png)
![]− ∞, h(m )[](Aexo_cu018x.png) ∪
∪![]− 2,− 1[](Aexo_cu019x.png) .
.
Étude de l’inéquation (3).
On considère la fonction φm définie par
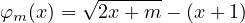
Il s’agit alors de discuter selon m de l’ensemble des x pour lesquels φm(x) ≥ 0.
On sait que la fonction est définie et continue dans 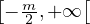 et que sa limite est
−∞ en +∞.
et que sa limite est
−∞ en +∞.
Considérons l’équation φm(x) = 0 :
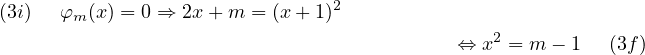 |
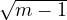 et bm =
et bm = 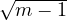 sont les solutions de (3f). De
plus
sont les solutions de (3f). De
plus
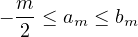
En effet, le signe de 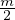 −
−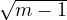 est le même que celui de
est le même que celui de
 |
Pour autant, am et bm ne sont pas forcément des solutions de (3i) car ils vérifient
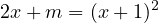
mais pas forcément
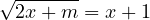
En fait bm + 1 > 0 donc bm est toujours solution de (3i) alors que
![√ -----
am + 1 ≥ 0 ⇔ m − 1 ≤ 1 ⇔ m ∈ [1,2]](Aexo_cu0121x.png)
Lorsque m ∈ [1,2], la fonction φm s’annule deux fois en an < bm et en changeant de signe (étude dérivée). L’ensemble des solutions est alors
![√ ----- √-----
[− m − 1, m − 1]](Aexo_cu0122x.png)
Lorsque m > 2, la fonction s’annule seulement en bn (en changeant de signe). L’ensemble des solutions est
![[− m-,√m-−-1]
2](Aexo_cu0123x.png)
Il faudrait examiner plus sérieusement les cas particuliers m = 1,2.