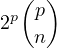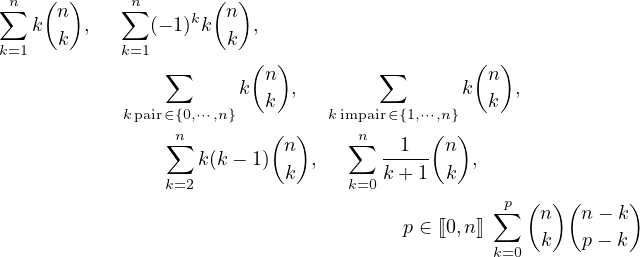
Énoncé
(Ecu11) Exprimer les sommes en fonction de n ≥ 2 :
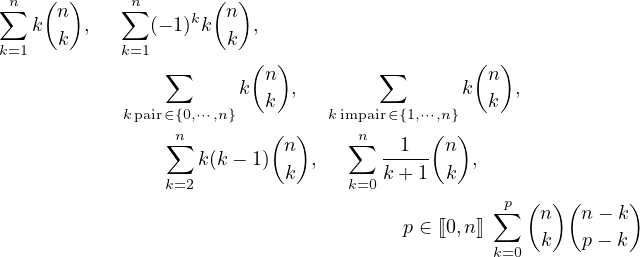 |
Corrigé
(Ecu11) Ces sommes se calculent de deux manières. En utilisant la relation entre coefficients du binôme
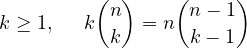
ou bien en dérivant des fonctions. Détaillons cette deuxième idée.
Définissons une fonction φ dans ℝ par :
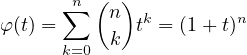
On en déduit, avec les règles de dérivation,
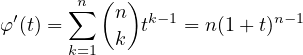
(le premier terme disparait en dérivant) On en déduit
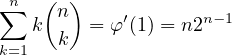
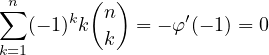
Notons
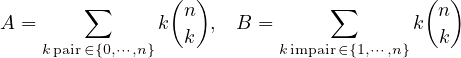
alors
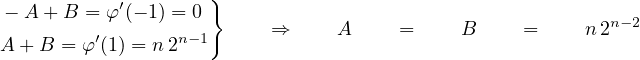 |
Calcul de ∑
k=2nk(k − 1)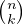 : à compléter.
: à compléter.
Calcul de ∑
k=0n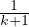
 : à compléter.
: à compléter.
Calcul de ∑
k=0p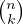
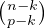 . On exprime les coefficients du binôme avec des
factorielles que l’on redistribue. On obtient
. On exprime les coefficients du binôme avec des
factorielles que l’on redistribue. On obtient