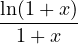 (3)
(3)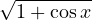 (4)
(4)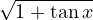 (3)
(3)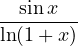 (3)
(3)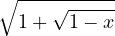 (2)
(2)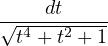 (10)
(10)Énoncé
(Ede01) Calculer un développement limité en 0 des fonctions suivantes à l’ordre indiqué entre parenthèses :
| 3sin2x − 2sin3x (4) | 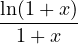 (3) (3) | |||||
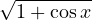 (4) (4) | ||||||
| esin x (3) | 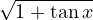 (3) (3) | |||||
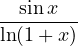 (3) (3) | tan2x2 (4) | |||||
| etan x (4) | 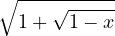 (2) (2) | |||||
∫
x3x2
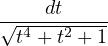 (10) (10) |
Corrigé
(Cde01)
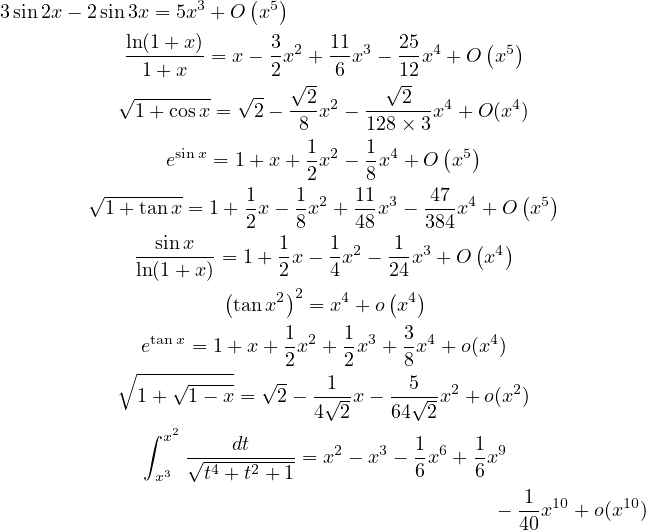 |