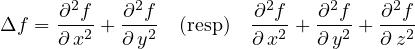
Énoncé
(Edg01) Soit U un ouvert de ℝ2 (resp ℝ3), une application numérique f définie dans U est dite harmonique si et seulement si Δf = 0 où
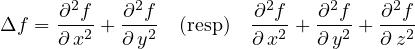
est le laplacien de f.
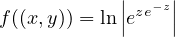
est harmonique.
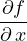 et y
et y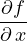 −x
−x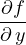 sont
harmoniques.
sont
harmoniques.
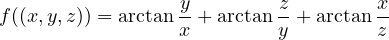
est harmonique sur ℝ∗3.
Corrigé
pas encore de corrigé