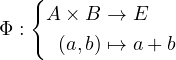
Énoncé
(Edi01) Soit A,B deux sous espaces vectoriels d’un espace vectoriel E, montrer la formule de Grassmann en utilisant l’application
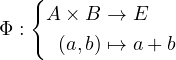
Corrigé
(Cdi01) On vérifie facilement que Φ est linéaire et que son image est A + B. Son noyau est formé par les couples (a,b) ∈ A × B tels que
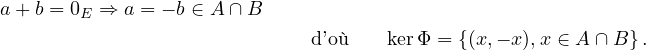 |
L’application de A ∩ B dans kerΦ qui à x associe (x,−x) est clairement un isomorphisme. On en déduit l’égalité des dimensions. Par le théorème du rang :
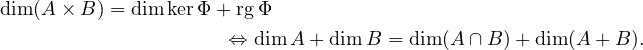 |