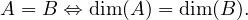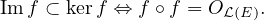
Énoncé
(Edi02) Soit f un endomorphisme d’un K-espace vectoriel de dimension finie E. Montrer que kerf = Imf si et seulement si f2 = 0ℒ(E) et 2rg(f) = dimE.
Corrigé
(Cdi02) Ici E est de dimension finie et f ∈ℒ(E).
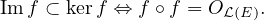
De plus, à cause du théorème du rang,
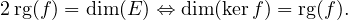
On a aussi : soit A et B deux sous-espaces tels que A ⊂ B, alors