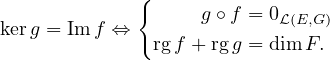
Énoncé
(Edi12) Soit E, F, G de dimensions finies, f ∈ℒ(E,F) et g ∈ℒ(F,G). Montrer que
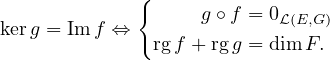
Corrigé
(Cdi12) Par définition de la composition :
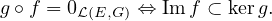
Donc kerg = Imf ⇒ g ∘ f = 0ℒ(E,G). De plus, d’après le théorème du rang appliqué à g
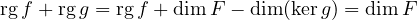
car rg f = dim(kerg).
Réciproquement,
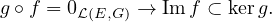
L’égalité des sous espaces vient de l’égalité des dimensions et du théorème du rang appliqué à g :
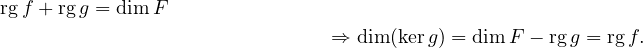 |