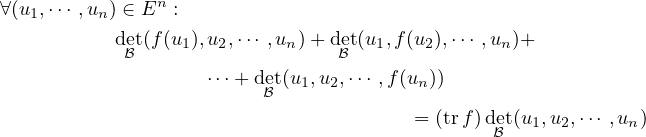
Énoncé
(Edt12) Soit E un K-espace vectoriel de dimension n, soit ℬ une base de E et f ∈ℒ(E). Montrer que
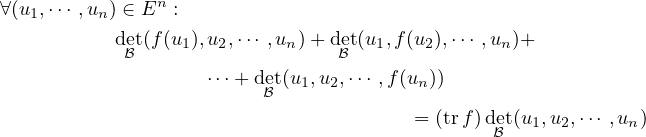 |
Corrigé
(Cdt12) On vérifie que l’application δ définie par :
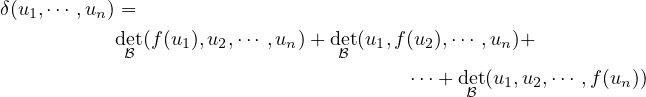 |
est multilinéaire et alternée. Il existe donc un λ tel que δ = λdet
B.Oncalculeλ en prenant pour ui les vecteurs de ℬ.