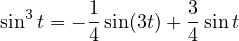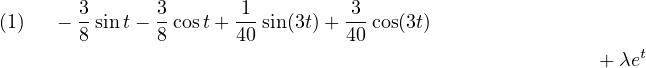
Énoncé
(ed01) Déterminer, pour les équations différentielles suivantes, les ensembles de solutions.
| (1) | y′(t) − y(t) = sin3t | ||||||
| (2) | y′(t) + 2ty(t) = et−t2 | ||||||
| (3) | y′(t) + y(t)cotan(t) = sint | ||||||
| (4) | (1 + t2)y′(t) + ty(t) = 1 + 2t2 | ||||||
| (5) | y′(t) + y(t) = tsint | ||||||
| (6) | y′(t) − iy(t) = ch(t) | ||||||
| (7) | y′(t) − iy(t) = cos(t) | ||||||
| (8) | y′(t) + y(t) = e−t + sint | ||||||
| (9) | y′(t) + y(t) = cos2t |
Chercher les solutions à valeurs réelles sauf pour (6) et (7) où l’on cherchera les solutions à valeurs complexes.
Corrigé
(Ced01) Solutions des équations différentielles proposées. Le paramètre λ est réel sauf pour (6) et (7) où il est complexe.
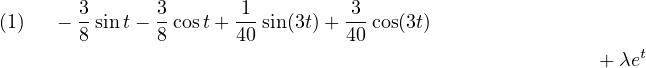 |
| (2) | et−t2 + λe−t2 | ||||||
| (3) | 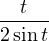 − −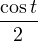 + + 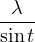 | ||||||
| (4) | x + 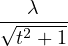 | ||||||
| (5) |  (sint − cost) + (sint − cost) +  cost + λe−t cost + λe−t | ||||||
| (6) |  sh(t) + sh(t) + 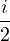 ch(t) + λeit ch(t) + λeit | ||||||
| (7) |  eit + eit +  e−it + λeit e−it + λeit | ||||||
| (8) | te−t − cost + cost +  sint + λe−t sint + λe−t | ||||||
| (9) |  + + 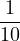 cos(2t) + cos(2t) +  sin(2t) + λe−t sin(2t) + λe−t |
Remarques sur les méthodes.
Pour l’équation (1), il faut commencer par linéariser le second membre. Deux
méthodes sont possibles.
Première méthode : utiliser sin2t = 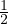 −
−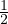 cos(2t) puis sinacosb =
cos(2t) puis sinacosb = 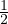
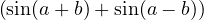 .
.
Deuxième méthode : utiliser la formule du binôme
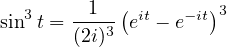
Par les deux méthodes, on trouve