Énoncé
(Eee01) Soit E euclidien, f une application de E dans E telle que (f(x)∕f(y)) = (x∕y) pour tout couple (x,y) de vecteurs de E. Montrer que f est linéaire et bijective.
Corrigé
Soit f une application qui n’est pas supposée linéaire mais qui conserve le produit scalaire. Pour tous vecteurs x et y, développons
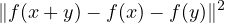
On obtient une somme de produits scalaires avec des f de chaque côté que l’on peut enlever par conservation du produit scalaire. Cela conduit au développement de
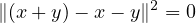
On montre de même que
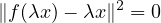
Une fois que l’on sait que f est linéaire, on montre qu’elle est injective en considérant la norme d’un vecteur du noyau puis qu’elle est bijective car un espace euclidien est de dimension finie.