
Énoncé
(Eef14) On note 𝒟 le ℂ-espace vectoriel des fonctions dérivables de ℝ dans ℂ. Soit f ∈𝒟. Pour chaque x ∈ ℝ, on note fx ∈𝒟 définie par :

On note V = Vect(fx, x ∈ ℝ) et on suppose dimV = 2.
Montrer que f′ et f′′ sont dans V . En déduire que f est solution d’une équation
différentielle linéaire d’ordre 2 à coefficients constants.
Corrigé
(Cef14)
Il existe x1 et x2 tels que (fx1,fx2) base de V .
Comme la famille est génératrice, il existe des fonctions à valeurs complexes λ1 et
λ2 telles que
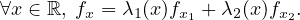
On va montrer que λ1 et λ2 sont dérivables. Pour cela on les exprime comme solutions d’un système de Cramer. Pour tout (x,t) ∈ ℝ2,
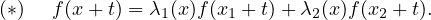
En particulier, pour tout t ∈ ℝ
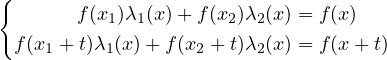
Le déterminant de ce système est
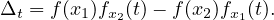
Comme (fx1,fx2) est libre, il existe t0 tel que Δt0≠0. Les expressions de λ1 et λ2
par les formules de Cramer montrent qu’elles sont dans V .
En dérivant (∗) une fois par rapport à x puis en prenant x = 0, on montre que
f′∈ V . On en déduit que f′ est dérivable. De plus, il existe des fonctions μ1 et μ2
vérifiant
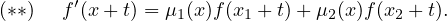
On montre de la même manière que μ1,μ2 ∈ V donc f′′∈ V .
La famille de trois vecteurs (f,f′,f′′) d’un espace de dimension 2 est liée (condition
suffisante de dépendance) donc f est solution d’une équation différentielle
linéaire d’ordre 2 à coefficients constants.