 ,pk des entiers naturels tels que
,pk des entiers naturels tels que
Énoncé
(Een09)
Soit p1, ,pk des entiers naturels tels que
,pk des entiers naturels tels que
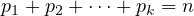
On désigne par c(n,p1, ,pk) le nombre de k-uplets (A1,
,pk) le nombre de k-uplets (A1, ,Ak) de parties
d’un ensemble E à n éléments telles que :
,Ak) de parties
d’un ensemble E à n éléments telles que :
A1 ∪ ∪ Ak = ⟦1,n⟧ ∪ Ak = ⟦1,n⟧ | ||||||
∀(i,j) ∈{1, ,k}2 ,k}2 | : i≠j ⇒ A i ∩ Aj = ∅ | |||||
∀i ∈{1, ,k} ,k} | : ♯Ai = pi |
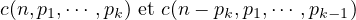
En déduire
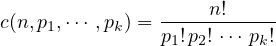
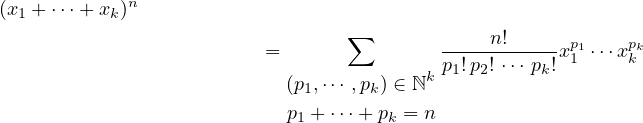 |
Corrigé
pas encore de corrigé