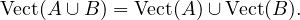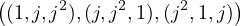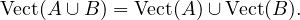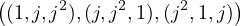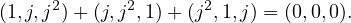Énoncé
(Eev01)
Étudier les propositions suivantes en démontrant celles qui sont vraies et en
donnant un contre-exemple pour les autres.
- ℝ2 muni de l’addition usuelle et de la loi externe sur ℝ α(x,y) = (αx,0)
est un ℝ espace vectoriel.
- L’ensemble des polynômes à coefficients réels divisibles par X2 + 1
est un ℝ espace vectoriel.
- Si A et B sont deux parties de E,
- La famille
n’admet aucune relation linéaire dans le ℂ espace vectoriel ℂ3.
Corrigé
(Cev01)
- Ce n’est pas un ℝ espace-vectoriel car la multiplication externe ne vérifie
pas 1(x,y) = (x,y).
- C’est bien un ℝ-espace vectoriel comme sous-espace de ℝ[X] car si des
polynômes sont divisibles par X2 + 1, leurs combinaisons linéaires
seront aussi divisibles.
- L’égalité est fausse en général car Vect(A ∪ B) est un sous-espace
alors que Vect(A)∪Vect(B) ne l’est que si Vect(A) ou Vect(B) est inclus
dans l’autre.
- Elle admet la relation linéaire