Énoncé
(Efc01)
Inégalité de Hölder.
Soit n > 1 un nombre entier et
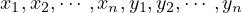
des réels strictement positifs. On se donne aussi un réel K > 0 un
entier s et on définit des réels λ1, ,λn en posant pour tout i entre 1 et
n :
,λn en posant pour tout i entre 1 et
n :
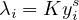
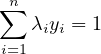
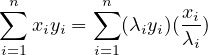
former une inégalité. Préciser s pour que l’exposant de yi disparaisse.
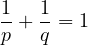
Démontrer l’inégalité de Hölder
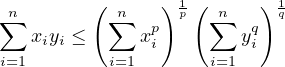
Corrigé
pas encore de corrigé