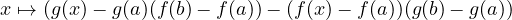![]a,b[](Aexo_gd010x.png) , on suppose que g′.
Montrer que g(b)≠g(a) et qu’il existe c ∈]a,b[ tel que
, on suppose que g′.
Montrer que g(b)≠g(a) et qu’il existe c ∈]a,b[ tel que
Énoncé
(Egd01)
Soit f et g des fonctions continues sur [a,b], dérivables sur ![]a,b[](Aexo_gd010x.png) , on suppose que g′.
Montrer que g(b)≠g(a) et qu’il existe c ∈]a,b[ tel que
, on suppose que g′.
Montrer que g(b)≠g(a) et qu’il existe c ∈]a,b[ tel que
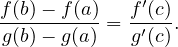
Corrigé
(Cgd01) Appliquer le théorème de Rolle à