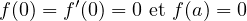
Énoncé
(Egd12) Soit f ∈𝒞1(0,+∞[) et a un réel strictement positif tels que :
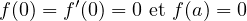
Montrer qu’il existe un point M du graphe (autre que l’origine) tel que la tangente en M passe par l’origine.
Corrigé
(Cgd12)
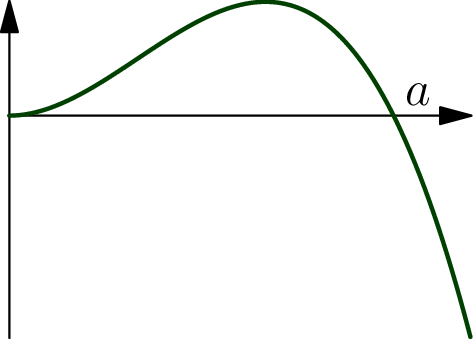
Soit m > 0 et M le point de coordonnées (m,f(m)). L’équations de la tangente au graphe en ce point est
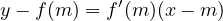
Elle passe par l’origine du repère si et seulement si
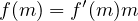
Il s’agit de montrer que, sous les hypothèses données, il existe un m > 0 tel que
f(m) = f′(m)m.
Considérons la fonction φ définie par :
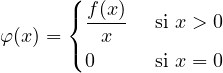
Par hypothèse, elle est continue en 0 et dérivable dans ]0,+∞[. De plus φ(0) = φ(a) = 0, on peut donc lui appliquer le théorème de Rolle entre 0 et a. Il existe un m > 0 tel que