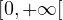 ) et f
) et f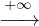 l ∈ ℝ. Soit 𝜀 > 0. Comme f
l ∈ ℝ. Soit 𝜀 > 0. Comme f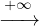 l, il existe A > 0 tel que
x ≥ A entraine
l, il existe A > 0 tel que
x ≥ A entraine 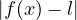 ≤
≤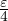 .
.Comme f restreinte à
![[0,A]](Aexo_is265x.png) est uniformément continue (thm de Heine), il existe
α > 0 tel, dans
est uniformément continue (thm de Heine), il existe
α > 0 tel, dans ![[0,A]](Aexo_is266x.png) , |y − x|≤ α entraine
, |y − x|≤ α entraine 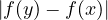 ≤
≤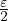 .
.Montrons que dans
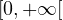 ,
,
Énoncé
(Eis26) Soit f une fonction continue dans ℝ+ et admettant une limite finie en +∞, montrer que f est uniformément continue.
Corrigé
(Cis26)
Ici f ∈𝒞(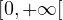 ) et f
) et f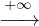 l ∈ ℝ. Soit 𝜀 > 0. Comme f
l ∈ ℝ. Soit 𝜀 > 0. Comme f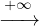 l, il existe A > 0 tel que
x ≥ A entraine
l, il existe A > 0 tel que
x ≥ A entraine 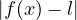 ≤
≤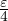 .
.
Comme f restreinte à ![[0,A]](Aexo_is265x.png) est uniformément continue (thm de Heine), il existe
α > 0 tel, dans
est uniformément continue (thm de Heine), il existe
α > 0 tel, dans ![[0,A]](Aexo_is266x.png) , |y − x|≤ α entraine
, |y − x|≤ α entraine 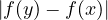 ≤
≤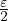 .
.
Montrons que dans 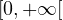 ,
,
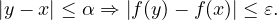
Si x et y sont dans ![[0,A ]](Aexo_is2611x.png) , cela résulte directement de la définition de
α.
, cela résulte directement de la définition de
α.
Si x et y sont dans 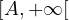 ,
,
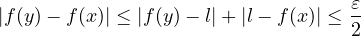
Si A est entre les deux. Par exemple x ≤ A ≤ y alors A − x ≤ y − x ≤ α donc
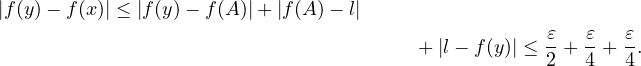 |