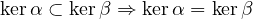
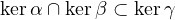
En considérant la restriction notée α′ de α à kerβ et la restriction notée γ′ de γ à kerβ, montrer qu’il existe une relation linéaire entre α, β, γ.
Énoncé
(Eml07)
Multiplicateurs de Lagrange.
Soit E un K espace vectoriel fixé. Sauf précision, toutes les formes linéaires sont
relatives à cet espace.
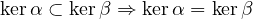
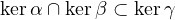
En considérant la restriction notée α′ de α à kerβ et la restriction notée γ′ de γ à kerβ, montrer qu’il existe une relation linéaire entre α, β, γ.
Corrigé
pas encore de corrigé