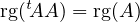
Énoncé
(Emo08) Soit A ∈ℳp,q(ℝ), montrer que
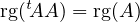
On pourra montrer que
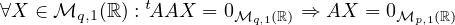
Corrigé
(Cmo08) Commençons par montrer l’implication suggérée
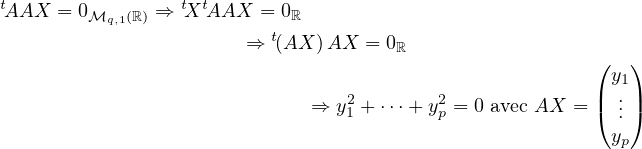 |
On en déduit ker(t AA) ⊂ ker(A).
L’inclusion réciproque étant évidente, les noyaux sont égaux. On conclut
en utilisant la version matricielle du théorème du rang : le rang d’une
matrice est égale à son nombre de colonne mois la dimension de son noyau.