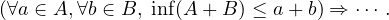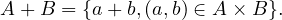
Énoncé
(Ere02) Soit A et B deux parties non vides et bornées de ℝ. On définit une partie de ℝ notée A + B par :
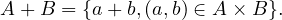
Montrer A + B est bornée et que
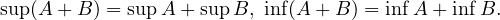
Corrigé
(Cre02) Pour tout s ∈ A + B, il existe (a,b) ∈ A × B tel que
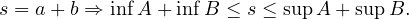
On en déduit que A + B est bornée et que
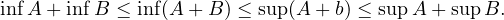
D’autre part, notons S = sup(A + B),
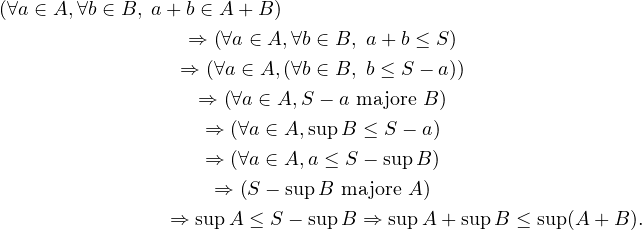 |
On en déduit supA + supB = sup(A + B).
L’égalité pour les bornes inférieures se démontre par une suite d’implications
analogues commençant par