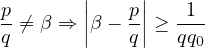
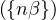 n∈ℕ sont deux à deux distinctes. On dira que la suite
est injective. En déduire
n∈ℕ sont deux à deux distinctes. On dira que la suite
est injective. En déduire 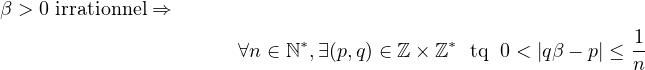 |
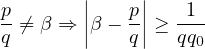
Montrer que β est rationnel.
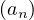 n∈ℕ et
n∈ℕ et 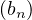 n∈ℕ d’entiers tels que
n∈ℕ d’entiers tels que
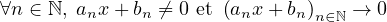
Énoncé
(Ere10) Critères d’irrationalité.
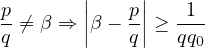
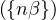 n∈ℕ sont deux à deux distinctes. On dira que la suite
est injective. En déduire
n∈ℕ sont deux à deux distinctes. On dira que la suite
est injective. En déduire 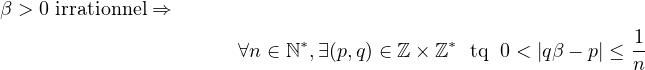 |
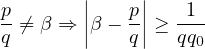
Montrer que β est rationnel.
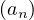 n∈ℕ et
n∈ℕ et 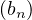 n∈ℕ d’entiers tels que
n∈ℕ d’entiers tels que
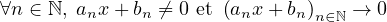
Corrigé
(Cre10) Critères d’irrationalité.
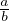 > 0 avec a et b ∈ ℕ∗. Alors
> 0 avec a et b ∈ ℕ∗. Alors
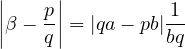
On peut donc prendre q0 = b car |qa − pb|≥ 1 (naturel non nul).
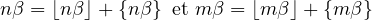
alors
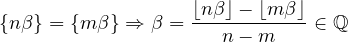
La suite injective 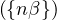 n∈ℕ prend une infinité de valeurs dans ]0,1[. Pour
tout n > 0, il existe (principe des tiroirs) des entiers distincts u et v tels
que
n∈ℕ prend une infinité de valeurs dans ]0,1[. Pour
tout n > 0, il existe (principe des tiroirs) des entiers distincts u et v tels
que
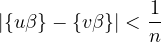
On en tire
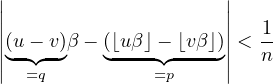
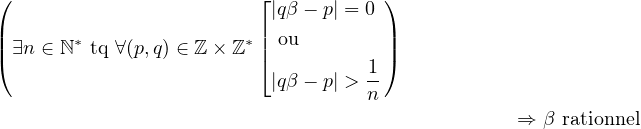 |
Lorsque β vérifie l’hypothèse de c. et en prenant un n > q0, la proposition entre parenthèse est vérifiée assurant que β est rationnel.