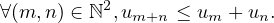
Énoncé
(Ere15)
Suites sous-additives. Lemme de Feteke.
Soit (un)n∈ℕ une suite de réels positifs, telle que
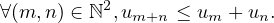
Montrer que (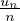 )n∈ℕ∗ converge vers inf{
)n∈ℕ∗ converge vers inf{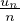 ,n ∈ ℕ∗}.
,n ∈ ℕ∗}.
(difficile, utiliser une division euclidienne.)
Corrigé
(Cre15)
Soit V = 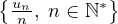 et l = inf V .
et l = inf V .
Il s’agit de la borne inférieure d’une partie non vide minorée par 0. Par définition
c’est un minorant de V donc
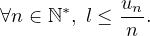
Soit 𝜀 > 0. Alors l + 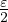 ≤ l est faux donc l +
≤ l est faux donc l + 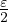 n’est pas un minorant de V (la
borne inférieure est le plus grand des minorants). Donc :
n’est pas un minorant de V (la
borne inférieure est le plus grand des minorants). Donc :
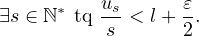
Écrivons la division euclidienne de n ∈ ℕ par s :
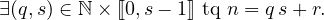
La condition de sous-additivité entraine
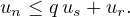
Notons M = max(u1,u2, ,us−1 et divisons par n :
,us−1 et divisons par n :
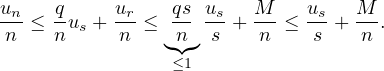
Comme la suite (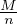 )n∈ℕ∗ converge vers 0,
)n∈ℕ∗ converge vers 0,
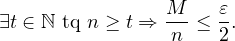
Soit N = max(s,t).
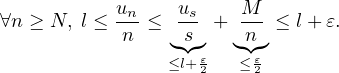
Voir le corrigé du problème Et si j’en achète plusieurs ? Combien pour chaque ? (http ://back.maquisdoc.net/v-1/index.php ?act=cheltid_elt=8876) sur les suites sous-additives