Énoncé
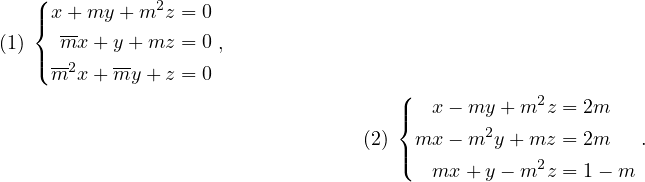
(Esl01) Le paramètre m et les inconnues x, y, z sont complexes. Discuter et résoudre les systèmes
 |
Corrigé
(Csl01)
En présence d’un paramètre, la multiplication d’une équation par une
expression contenant le paramètre n’est pas une opération élémentaire et ne
conserve pas l’ensemble des solutions. On ne doit pas utiliser ce genre de
transformation.
Système (1).
En utilisant L3 ← L3 −mL2, L2 ← L2 −mL1, on obtient un système triangulaire
équivalent
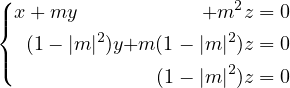
Si |m|≠1, le système admet une unique solution. Si |m| = 1, le système est équivalent àla seule équation
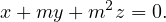
Système (2).
En utilisant L3 ← L3 − L2, L2 ← L2 − mL1, L2 ↔ L3, on obtient un système
triangulaire équivalent
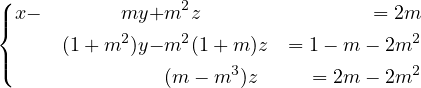
On présente les ensembles de solutions dans les différents cas après
calculs.
Si m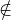
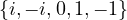 ,
,
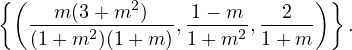
Si m = 0.
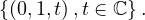
Si m = 1.
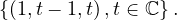
Si m ∈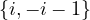 , pas de solution.
, pas de solution.