Énoncé
(Esl06) Soit λ, μ, γ, δ des nombres complexes tels que λ≠μ et γδ≠0. On définit des fonctions g et g′ de ℝ dans ℂ par :
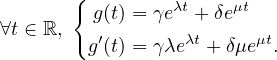
Pour tous α et β complexes, on définit f par
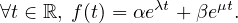
En utilisant les formules de Cramer, exprimer des complexes K et K′ tels que
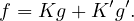
Corrigé
(Csl06) En combinant les définitions, on montre qu’il suffit que K et K′ vérifient
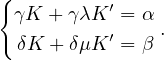
Il s’agit d’un système de Cramer de déterminant
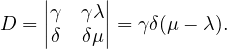
D’après les formules de Cramer,
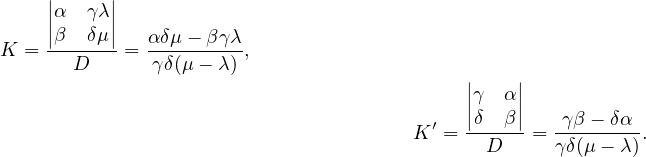 |