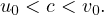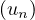 n∈ℕ et
n∈ℕ et  n∈ℕ définies par
récurrence par
n∈ℕ définies par
récurrence par
Énoncé
(Esr04)
Soit a et b réels strictement positifs fixés. Déterminer une condition nécessaire
et suffisante sur u0 et v0 pour que les suites 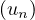 n∈ℕ et
n∈ℕ et  n∈ℕ définies par
récurrence par
n∈ℕ définies par
récurrence par
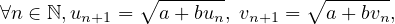
soient adjacentes.
Corrigé
(Csr04) Définissons des fonction f et φ dans
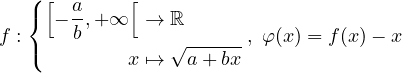
La fonction f est croissante et admet un unique point fixe
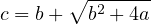
On peut déterminer le signe de f(x) − x.
−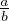 | c | +∞ | |||
| f(x) − x | + | 0 | − |
On se trouve dans le cas de l’étude traitée en cours. La condition assurant que les suites sont adjacentes est donc