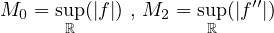
Énoncé
(Etl01) Soit f ∈𝒞2(ℝ) avec f et f′′ bornées. On note
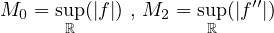
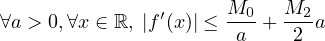
On pourra utiliser deux fois une formule de Taylor (quel reste ?) à l’ordre 2 en considérant les points x, x − a, x + a.
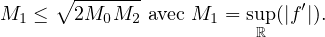
![(| x2
|{1 − 2 si x ∈ [− 2,0]
f (x) = | 2+ x2 .
|( 2(1-+-x2) si x > 0](Aexo_tl013x.png)
Montrer que f est 𝒞2 et calculer M0, M1, M2. Que peut-on en conclure pour l’inégalité du b. ?
Corrigé
(Ctl01)
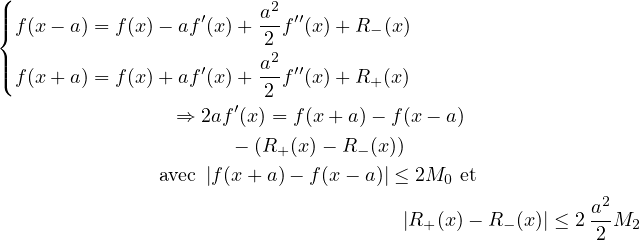 |
par l’inégalité de Taylor Lagrange. On en déduit l’inégalité demandée.
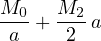
est un majorant de |f′|. Le meilleur majorant que l’on peut obtenir ainsi est la plus petite valeur de la fonction
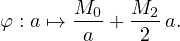
On forme le tableau de variations de la fonction

La fonction est décroissante puis croissante. Elle atteint sa plus petite valeur
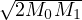 en
en 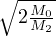 .
.
![(
′ { − x si − x ∈ [− 2,0]
f (x) = ( −----x--- si x ∈ [0,+ ∞ [
(1 +x2)2](Aexo_tl0110x.png)
![(
′′ |{ − 1 si − x ∈ [− 2,0]
f (x) = | 3x2-−-1-
( − (1 + x2)3 si x ∈ [0,+∞ [](Aexo_tl0111x.png)
On constate que les fonctions se raccordent bien et que f est donc 𝒞2.
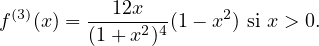
On en déduit M0 = M1 = 2 et M2 = 1 qui sont atteints en −2 et non aux
extréma locaux (0, 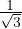 ,
, 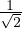 ). Cette fonction vérifie M1 =
). Cette fonction vérifie M1 = 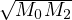 mais elle
n’est pas dans 𝒞2(ℝ) donc on n’a pas montré que l’inégalité du b. est
optimale.
mais elle
n’est pas dans 𝒞2(ℝ) donc on n’a pas montré que l’inégalité du b. est
optimale.