![∫
π-π- π
∀a ∈ ]− 2,2 [, f (a) = 0 tan(a sinx)dx](Aexo_tl070x.png)
Énoncé
(Etl07) On définit une fonction f par :
![∫
π-π- π
∀a ∈ ]− 2,2 [, f (a) = 0 tan(a sinx)dx](Aexo_tl070x.png)
Montrer que, en 0,
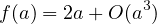
Former un développement limité à l’ordre 3 de f en 0
Corrigé
(Ctl07) Toute formule de Taylor est une formule de Taylor idiote. Par exemple
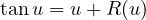
où R est le reste c’est à dire
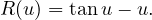
Ce qui fait l’utilité d’une formule de Taylor c’est l’information dont on dispose sur le reste. Il n’est pas intéressant d’introduire trop tôt ce renseignement dans le contexte d’une intégrale.
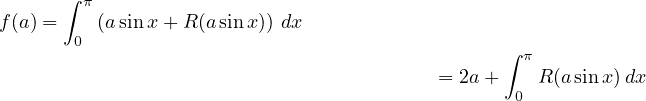 |
On connait les développements limités de tan. On en déduit une information sur le reste
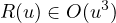
que l’on traduit sous une forme adaptée à l’utilisation dans l’intégrale. Il existe une fonction φ définie au voisinage de 0 telle que
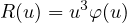
La fonction φ est localement bornée en 0. Il existe α > 0 et Φ > 0 tels que
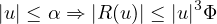
On en déduit, en majorant l’intégrale,
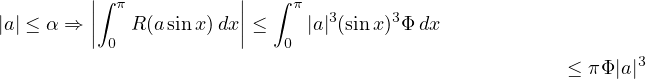 |