Énoncé
(Evc01)
Définition de l’exponentielle
complexe1
On rappelle que, si a est un nombre réel, on note
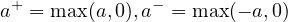
On a alors a = a+ − a−.
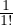 r +
r + 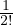 r2 +
r2 +  +
+ 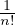 rn)
n∈ℕ.
rn)
n∈ℕ.
| sn | = u0 + u1 +  + un + un | ||
| Sn | = |u0| + |u1| +  + |un|. + |un|. |
Montrer que la convergence de la suite à valeurs réelles (Sn)n∈ℕ entraîne celle de la suite complexe (sn)n∈ℕ. Dans toute la suite et pour tout z ∈ ℂ, on note
| sn(z) | = 1 + 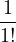 z + z + 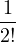 z2 + z2 +  + +  zn, zn, | ||
| Sn(z) | = 1 + 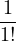 |z| + |z| + 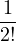 |z|2 + |z|2 +  + + 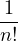 |z|n |z|n | ||
| = sn(|z|) |
 |

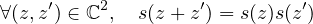
En fait on définit la fonction exponentielle complexe en posant exp(z) = s(z) pour tout nombre complexe z. On vient de démontrer certaines des propriétés admises en début d’année lors de la présentation des fonctions usuelles.
Corrigé
pas encore de corrigé